Leetcode 1386. Cinema Seat Allocation

 1386. Cinema Seat Allocation

Medium, Arrays

A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.

Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.

 

Example 1:

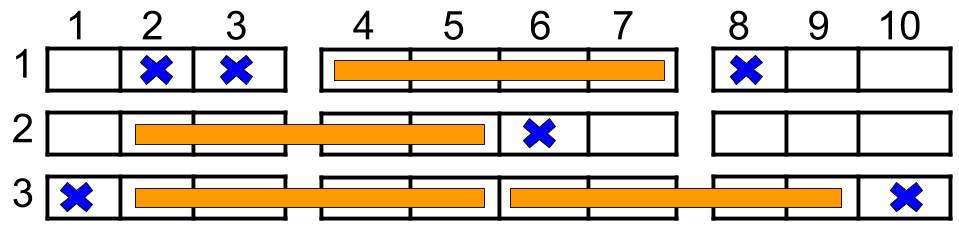
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3:

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

 

Constraints:

• 1 <= n <= 10^9
• 1 <= reservedSeats.length <= min(10*n, 10^4)
• reservedSeats[i].length == 2
• 1 <= reservedSeats[i][0] <= n
• 1 <= reservedSeats[i][1] <= 10
• All reservedSeats[i] are distinct.

Problem Statement:

You are tasked with assigning four-person groups to a cinema with n rows of seats. Each row contains 10 seats labeled from 1 to 10. Groups can only sit together if they occupy four adjacent seats in the same row, and these seats should not include any reserved ones.

You are given:

• n: the number of rows in the cinema.
• reservedSeats: an array of reserved seat positions, where each element is [row, seat].

Your goal is to determine the maximum number of four-person groups that can be assigned while following the rules.

Key Observations:

1. Seats Configuration:

   • A row can accommodate a group of 4 in the following configurations:
     • Left Block: Seats 2-5.
     • Middle Block: Seats 4-7.
     • Right Block: Seats 6-9.

2. Edge Cases:

   • If a reserved seat falls within a block, that block cannot host a group.
   • Multiple blocks can coexist if their seat ranges do not overlap.

3. Constraints:

   • $n$ can be very large (up to $10^9$), but the reserved seats are significantly smaller in number.
   • We only need to check rows with reserved seats, as the rest can accommodate two groups per row.

---

Approach Explanation:

1. Mapping Reserved Rows:

   • Use a dictionary to map each row to a set of reserved seat numbers.

2. Checking Block Availability:

   • For each row in the dictionary:
     • Check whether each block (Left, Middle, Right) is free from reserved seats.
   • Calculate the number of groups for that row.

3. Unreserved Rows:

   • Rows without reserved seats can accommodate two groups per row.

4. Complexity:

   • Time Complexity: $O(r \cdot k)$, where $r$ is the number of rows with reserved seats, and $k$ is the average number of reserved seats per row.
   • Space Complexity: $O(r)$, for storing the mapping of reserved seats.

---

Solution in C#:

using System;
using System.Collections.Generic;

public class Solution
{
    public int MaxNumberOfFamilies(int n, int[][] reservedSeats)
    {
        // Step 1: Map rows to reserved seats
        var reservedMap = new Dictionary<int, HashSet<int>>();
        foreach (var seat in reservedSeats)
        {
            int row = seat[0], col = seat[1];
            if (!reservedMap.ContainsKey(row))
                reservedMap[row] = new HashSet<int>();
            reservedMap[row].Add(col);
        }

        // Step 2: Calculate the maximum number of groups
        int maxGroups = 0;

        // Check rows with reserved seats
        foreach (var kvp in reservedMap)
        {
            var reserved = kvp.Value;

            // Check blocks
            bool leftBlock = !reserved.Overlaps(new HashSet<int> { 2, 3, 4, 5 });
            bool middleBlock = !reserved.Overlaps(new HashSet<int> { 4, 5, 6, 7 });
            bool rightBlock = !reserved.Overlaps(new HashSet<int> { 6, 7, 8, 9 });

            if (leftBlock && rightBlock)
                maxGroups += 2; // Two groups can fit
            else if (leftBlock || middleBlock || rightBlock)
                maxGroups += 1; // Only one group can fit
        }

        // Step 3: Add rows without reserved seats
        maxGroups += 2 * (n - reservedMap.Count);

        return maxGroups;
    }
}

---

Example Walkthrough:

Input:

n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]

Execution:

1. Reserved Map:

   {
       1: {2, 3, 8},
       2: {6},
       3: {1, 10}
   }
   

2. Row 1:

   • Left Block: Blocked (2, 3 are reserved).
   • Middle Block: Free.
   • Right Block: Blocked (8 is reserved).
   • Groups: 1.

3. Row 2:

   • Left Block: Free.
   • Middle Block: Blocked (6 is reserved).
   • Right Block: Free.
   • Groups: 2.

4. Row 3:

   • Left Block: Free.
   • Middle Block: Free.
   • Right Block: Free.
   • Groups: 2.

5. Add Remaining Rows: No unreserved rows.

Output:

4

---

Complexity Analysis:

• Time Complexity: $O(r \cdot k)$, where $r$ is the number of rows with reserved seats, and $k$ is the average reserved seats per row.
• Space Complexity: $O(r)$, for the reserved seat mapping.