Leetcode 64. Minimum Path Sum

 64. Minimum Path Sum

Medium, Arrays

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

 

Example 1:

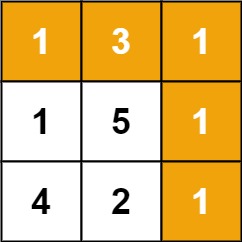
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

To solve the problem "64. Minimum Path Sum", we aim to find a path from the top-left corner of a grid to the bottom-right corner such that the sum of all numbers along the path is minimized. Only moves to the right or downward are allowed.

---

Approach 1: Dynamic Programming (2D DP Array)

Explanation:

• We can use a 2D DP array dp where dp[i][j] represents the minimum path sum to reach cell (i, j).
• The recurrence relation is:
  • If at the first cell: $dp[0][0] = grid[0][0]$.
  • If in the first row: $dp[0][j] = dp[0][j-1] + grid[0][j]$.
  • If in the first column: $dp[i][0] = dp[i-1][0] + grid[i][0]$.
  • Otherwise: $dp[i][j] = \text{grid}[i][j] + \min(dp[i-1][j], dp[i][j-1])$.

Code:

public class Solution {
    public int MinPathSum(int[][] grid) {
        int m = grid.Length;
        int n = grid[0].Length;

        int[,] dp = new int[m, n];
        dp[0, 0] = grid[0][0];

        // Fill first row
        for (int j = 1; j < n; j++) {
            dp[0, j] = dp[0, j - 1] + grid[0][j];
        }

        // Fill first column
        for (int i = 1; i < m; i++) {
            dp[i, 0] = dp[i - 1, 0] + grid[i][0];
        }

        // Fill the rest of the grid
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i, j] = grid[i][j] + Math.Min(dp[i - 1, j], dp[i, j - 1]);
            }
        }

        return dp[m - 1, n - 1];
    }
}

---

Approach 2: Dynamic Programming (In-Place Modification)

Explanation:

• Instead of using an additional DP array, we can reuse the input grid itself to save space.
• The logic remains the same, but we overwrite the grid cells with the minimum path sums.

Code:

public class Solution {
    public int MinPathSum(int[][] grid) {
        int m = grid.Length;
        int n = grid[0].Length;

        // Update the first row
        for (int j = 1; j < n; j++) {
            grid[0][j] += grid[0][j - 1];
        }

        // Update the first column
        for (int i = 1; i < m; i++) {
            grid[i][0] += grid[i - 1][0];
        }

        // Update the rest of the grid
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                grid[i][j] += Math.Min(grid[i - 1][j], grid[i][j - 1]);
            }
        }

        return grid[m - 1][n - 1];
    }
}

---

Approach 3: Optimized Space (Single Row DP)

Explanation:

• Instead of using a 2D DP array, maintain a single array dp of size $n$, representing the minimum path sum for the current row.
• As we iterate through each row, update the dp array in-place based on the values from the current row and the previous row.

Code:

public class Solution {
    public int MinPathSum(int[][] grid) {
        int m = grid.Length;
        int n = grid[0].Length;

        int[] dp = new int[n];
        dp[0] = grid[0][0];

        // Fill the first row
        for (int j = 1; j < n; j++) {
            dp[j] = dp[j - 1] + grid[0][j];
        }

        // Process each row
        for (int i = 1; i < m; i++) {
            dp[0] += grid[i][0]; // Update the first column value
            for (int j = 1; j < n; j++) {
                dp[j] = grid[i][j] + Math.Min(dp[j], dp[j - 1]);
            }
        }

        return dp[n - 1];
    }
}

---

Comparison of Approaches:

Approach	Time Complexity	Space Complexity	Notes
2D DP Array	$O(m \times n)$	$O(m \times n)$	Straightforward, easy to debug.
In-Place Modification	$O(m \times n)$	$O(1)$	Reuses the grid, saves space.
Single Row DP (Optimized)	$O(m \times n)$	$O(n)$	Best for large grids.

All approaches have the same time complexity but differ in space usage. Use the in-place or single-row DP for optimal performance in terms of memory.